Data Structure: tree

Table of Contents

简要介绍 #

之前讨论的数据结构:数组、链表、栈和队列在逻辑上都属于线性结构。这些本质上都是数据按照顺序排列的不同集合类型，如下图所示，这些结构都有明显的逻辑起点和终点。

集合中每个元素都可能有前驱或者后继元素，因此它们都呈现线性或顺序排列特征。这些所谓的数据结构是计算机存储和组织数据的方式，选择不同的数据结构去存储和组织数据是决定一个程序运行高效的基础。这个有很多个因素

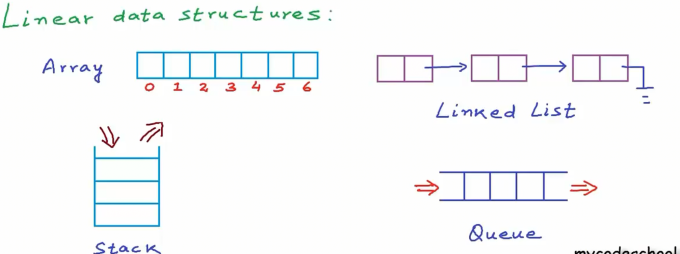
数据类型特性：特定数据结构可能最适配某种数据类型
操作成本：在一般情况下，我们是希望优化高频操作的成本，例如对于需要频繁检索的列表，可将其存储为排序数组，这样就可以执行二分查找等操作
内存消耗也是一个主要的因素，有时是需要降低内存占用

树结构常用于表示层次化数据，例如展示一个企业组织架构中人员层级关系时，可这样呈现，下图是一家公司的组织层级示意

在这家公司中，John是CEO，他有两名直接下属：Steve和Rama。Steve也有三个直接下属，他是Lee、Bob、Ella的经理。Rama也有两名直接下属，而Bob有两名直接下属，Tom则有一名直接下属。这个绘制特定逻辑结构就是一棵树，其实我们需要将这个结构倒过来看，这样他就更像一颗真实的树。树的根节点位于顶部，分支结构是向下延伸的，树数据结构的逻辑表示通常都是这样。根在顶端，分支向下延伸，因此树是存储和组织天然分层数据的高效方式。但是这并非是树在计算机科学中的唯一应用，后续将讨论其他应用场景及实现细节，比如如何在计算机内存中构建这种逻辑结构。在此之前，我想先将树定义为逻辑模型。树数据结构可定义为：通过节点实体相互链接形成的层次结构集合。 树属于非线性数据结构，具有层次化特性。最顶层的节点成为根节点。每个节点都存储着任意类型的数据，在当前示例中，节点存储的是员工姓名和职位信息。因此可以创建一个结构体，里面包含了两个字符串字段的对象，分别存储姓名和职位信息。每个节点除存储数据外，还可能包含指向其他节点的链接或引用，这些节点称为其子节点。介绍一下树数据结构中的一些专业术语。

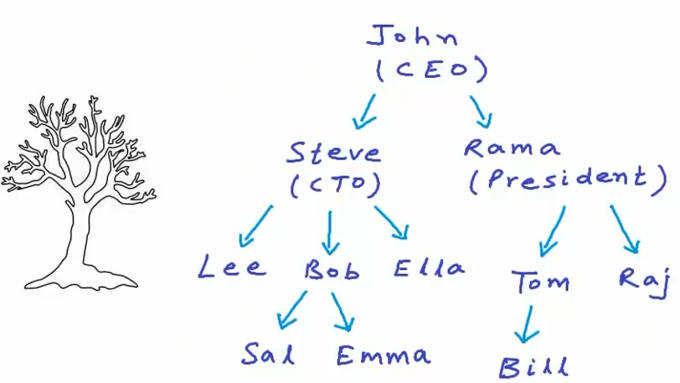
树中的术语 #

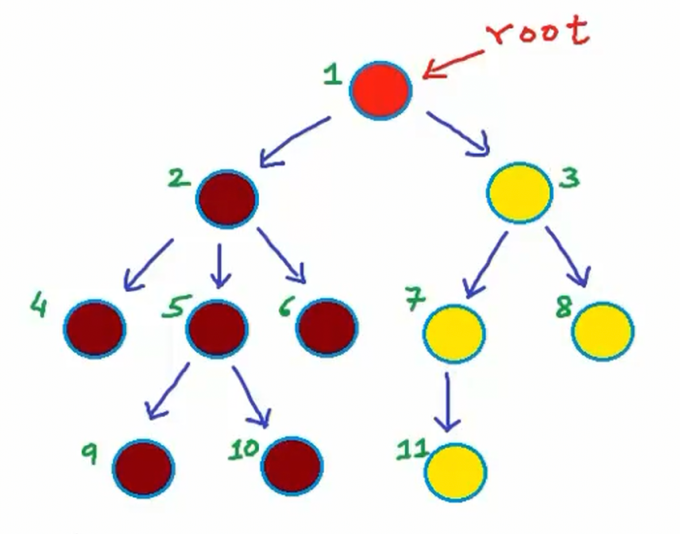
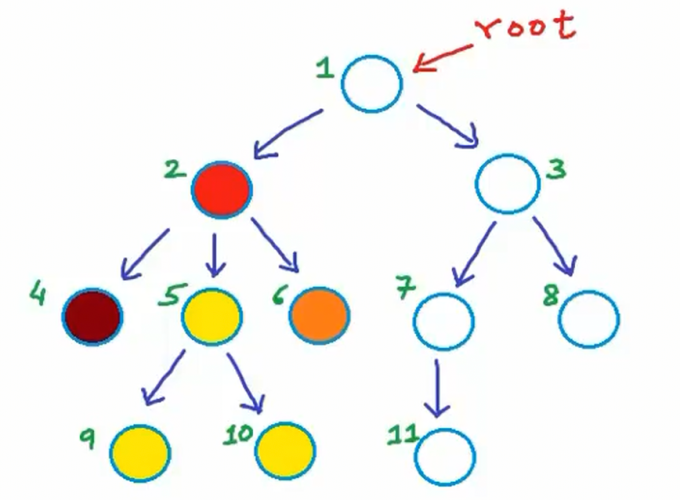
将上图中的各个节点进行编号，以便后续引用。仅仅是为了方便讲解，并不代表确定的顺序关系

每个节点都会存储数据，数据类型不限，可以是整型、字符或字符串。为了简化示意，图中不展示具体数据内容。如前面所说，节点可通过链接指向其他节点，这些节点被称为子节点。图示中的每个箭头都代表一个链接。1号节点称为根节点(root)，根节点连接着2号与3号节点，因此节点2和3是节点1的子节点，节点1则是节点2和3的父节点。已经提到了根节点(root)、子节点(children)和父节点(parent)。根节点是唯一没有父节点的节点。在此树结构中，节点1是节点2和3的父节点，节点2是节点1的子节点。现在节点4、5、6是节点2的子节点，因此节点2既是节点1的子节点，又是节点4，5，6的父节点。同一父节点的子节点互为兄弟节点。节点2和3是兄弟节点，4、5、6是兄弟节点，7和8是兄弟节点，9和10是兄弟节点。 没有子节点的节点称为叶子节点，图中的4、6、9、10、8、11都是叶子节点。至少有一个子节点的其他节点可称为内部节点，图中的1、2、3、5、7都是内部节点。还可以定义更多关系，例如父节点的父节点可称为祖父节点，因此节点1是节点4的祖父节点，节点4是节点1的孙节点。通常，若通过链接从节点A可达节点B(需注意这些链接并非双向)，例如存在1->2的链接，则只能从1到2，而不能从2到1。在树结构中移动时，我们只能沿单一方向遍历。综上，若从节点A到达节点B，则A称为B的祖先节点，B称为A的后代节点。以节点10为例，节点1、2、5均为节点10的祖先节点。节点10则是所有这些节点的后代节点。

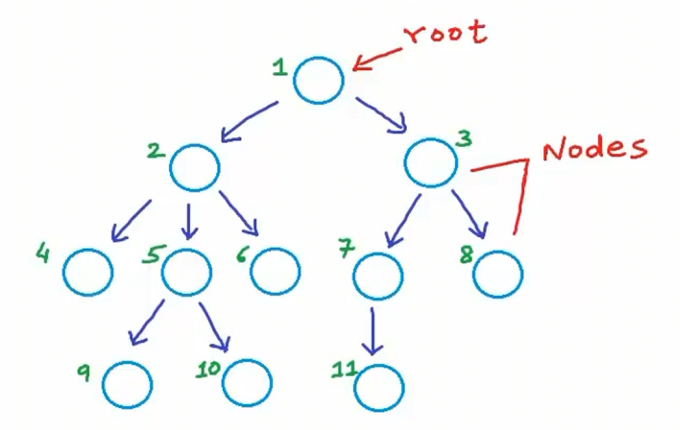
问题一：节点4和9的共同祖先是哪些节点？节点4的祖先节点是节点1、2，节点9的祖先节点是节点1、2、5，那么它们的共同祖先节点是节点1、2。
问题二：节点6和7是否为兄弟节点？不是兄弟节点，因为它们的父节点不同，但是它们有另外一层关系，它们是堂兄弟。父节点不同但祖父节点相同的节点可互称为堂兄弟节点。节点3是节点6的叔节点 – 因为它是节点2(节点6的父节点)的兄弟节点。

树的若干特性 #

树可定义为递归数据结构，其递归定义为由根节点及若干子树构成的结构。

具体而言，树根节点包含指向所有子树根节点的链接。图中T1、T2、T3即为子树。在之前绘制的图结构中，根节点下包含两个子树。

根节点标记为红色，左侧子树为棕色，右侧子树为黄色。我们还可以进一步拆分左侧子树，此时2号节点称为该子树的根节点。以2号节点为根的子树包含三个子结构。这三个子结构分别用不同颜色标识。

递归本质上是以自相似的方式进行问题简化，树的这种递归特性将贯穿所有应用场景，无论是树的实现还是具体应用。

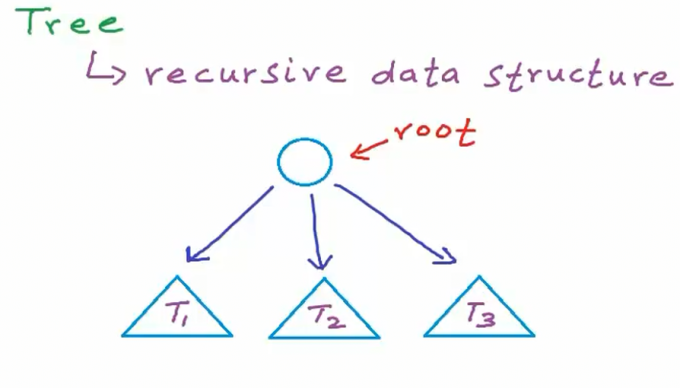
节点与边的关系 #

接下来讨论的特性是：具有n个节点的树必然包含n-1条链接(或称为边)，如果大于n-1则这个树必然成环。图示中每个箭头都代表一条链接或边。除根节点外，所有节点都有且仅有一条入边，以2号节点为例，它只有一条入边，但它有三个子节点，分别是节点4、5、6，有三个出边。每条父子关系对应一条链接，因此，在有效树结构中，n个节点必然对应n-1条边。

深度和高度 #

讨论深度(depth)和高度(height)这两个属性。

深度 #

No. of edges in path from root to x

节点X的深度定义为从根节点到X的路径长度(Depth of some node X in a tree can be defined as length of the path from root to node X)，路径上的每条边会使长度增加一个单位。因此也可表述为"根节点到X路径上的边数"。根节点的深度值为0. 对于5号节点，从根节点到它的路径包含两条边，因此该节点深度为2。当前树结构中：节点2和3深度为1，节点4、5、6、7、8深度为2，节点9、10、11深度为3。

高度 #

No. of edges in longest path from x to a leaf.

节点高度的定义：从该节点到叶节点的最长路径所含边数。因此节点X的高度等于从X到叶节点的最长路径中包含的边数。以节点3为例，从节点3到节点8的边数为1，从节点3到节点11的边数为2，那么从节点2到节点11的路径是最长路径，边数为2，因此节点3的高度为2。

所有叶节点的高度均为0。

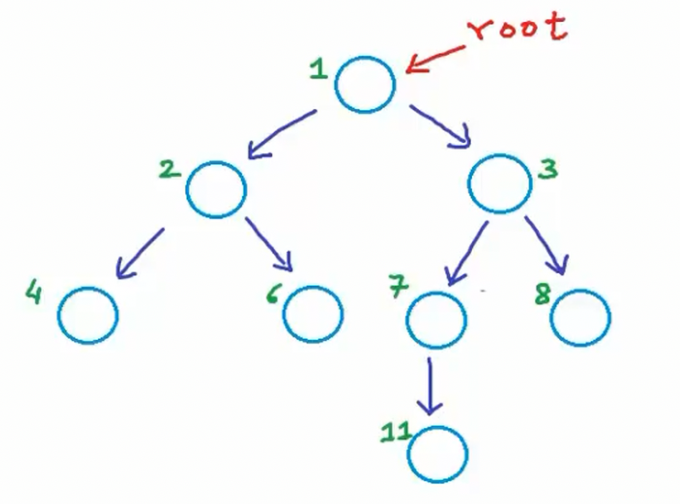
那么这棵树的根节点高度是多少呢？那么你就计算从根节点到所有叶子路径的路径长度，选出一个最长的路径，它的边数就是根节点的高度，所有叶子节点分别是4、6、9、10、8、11，到4的边树为2，到9、10、11的边数为3，到8的边数为2，那么根节点的高度就为3。 根节点的高度就是树的高度。高度和深度是不同属性，节点的高度和深度可能相同也可能不同。根据特性，树结构可分为多种类型，不同场景会使用不同种类的树结构。最简单常见的树结构要求每个节点最多只能只能有两个节点。如下图，这就是典型的二叉树结构，一个节点最多有两个节点。

二叉树是最重要的树结构，最常用的实现方式是通过指针或引用动态连接节点，类似于链表的实现方式。如图所示，节点包含三个字段，中间单元用于存储数据，左侧单元存储左子节点地址，右侧单元存储右子节点地址。由于这是二叉树结构，每个节点最多只能拥有两个子节点。我们可以将这两个子节点分别称为左子节点和右子节点。

在C/C++中，可以使用结构体的方式定义一个二叉树的节点。

1
2
3
4
5
struct Node {
    int* data;
    Node* left;
    Node* right;
};

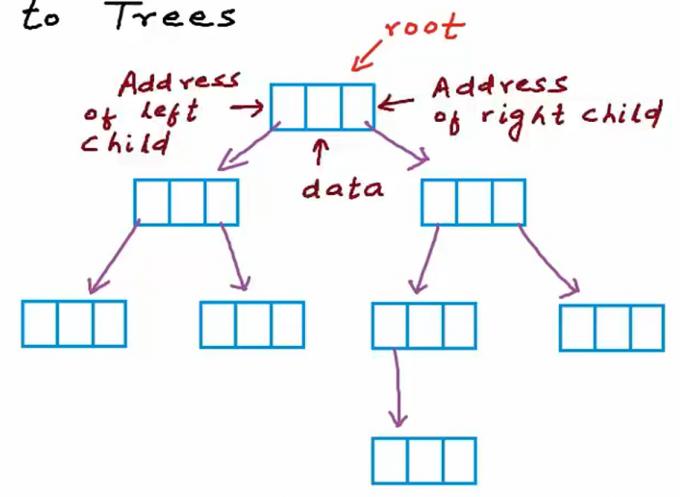
整型变量存储数据，两个指针分别指向左子树根节点(左子节点地址)和右子树根节点(右子节点地址)。仅设置两个指针是因为二叉树最多只能拥有两个子节点。这种节点的定义仅适用于二叉树。对于可包含任意数量子节点的通用树结构，会采用其他实现方式。要记住，存储天然层级数据并非树的唯一应用场景。简单了解一下树结构在计算机科学中的典型应用:

存储天然层级数据(storing naturally hierarchical data)。例如磁盘驱动器中的文件系统，其文件与文件夹的层级关系就是典型的层级数据。这类数据就是以树结构进行存储的。
组织数据集合，实现快速搜索、插入和删除操作(organize data for quick search,insertion,deletion)。比如后续的二叉搜索树，其元素搜索时间复杂度仅仅为对数级(O(logn))
特殊结构的Trie树常用于字典存储，这种数据结构高效快速，可用于实现动态拼写检查功能。还可应用于网络路由算法