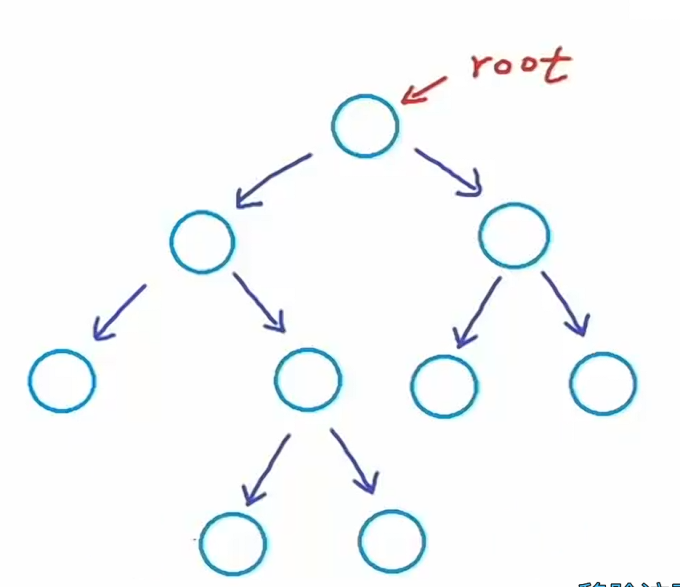
二叉树 # 如前所述,二叉树的特性在于每个节点最多只能拥有两个子节点。先介绍二叉树的基本特性,再重点讨论特殊类型,比如用于存储有序数据的高效数据结构 – 二叉搜索树。
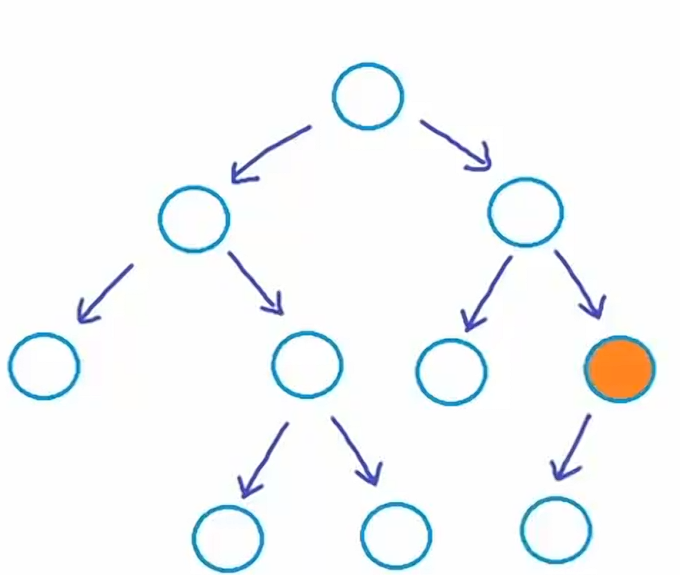
如图所示,当前树结构的节点均包含零个或者两个子节点。但二叉树也是允许存储仅有一个子节点的情况,现在新增一个节点,最右侧的叶子节点就拥有一个属于自己的子节点。
仅含单个节点的树也属于二叉树
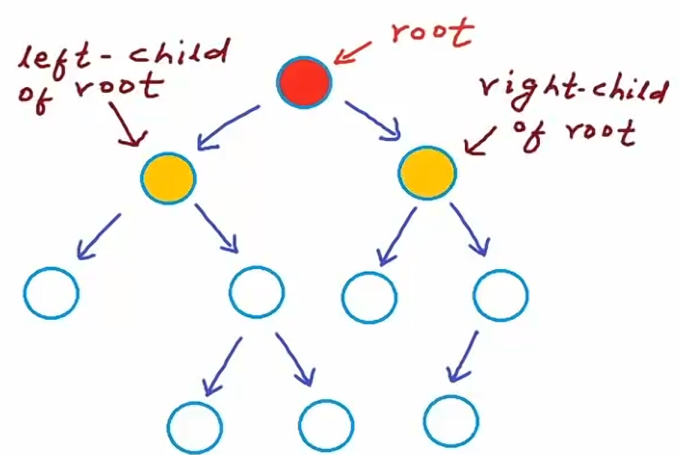
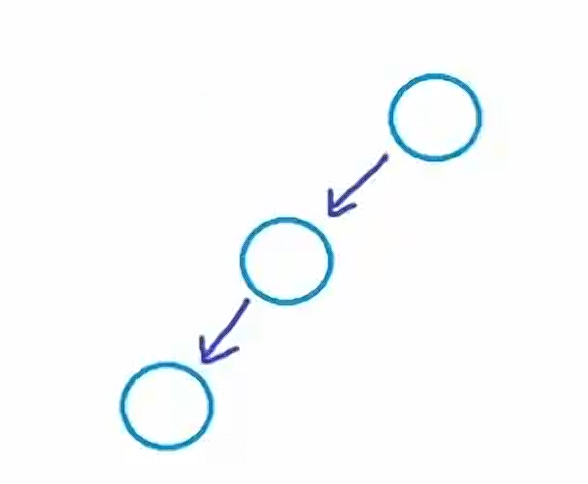
类似左侧排列的这种结构也是二叉树
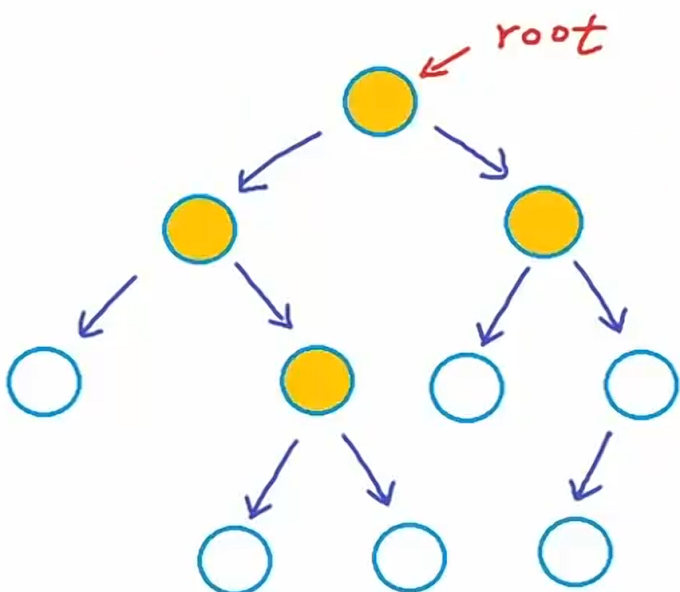
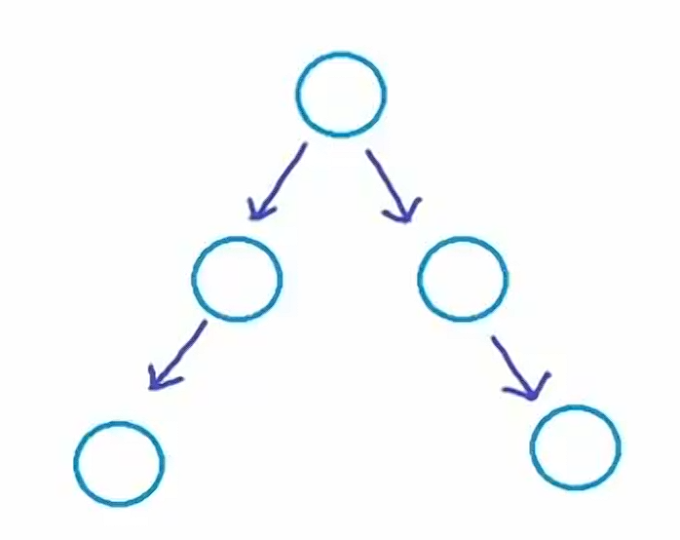
下图也是一个二叉树
核心约束在于:任何节点至多只能拥有两个孩子节点 严格二叉树 # 当前仅当每个节点有零或两个孩子节点时,才称为严格二叉树或者真二叉树
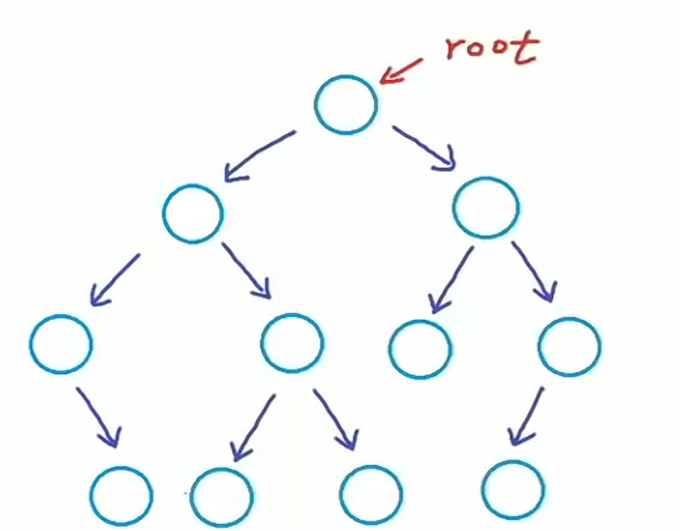
下图中的结构就不是一个严格的二叉树,因为存在两个仅有一个孩子的节点。
完全二叉树 # 定义完全二叉树的标准是:除最底层外各层完全填满,且最底层节点尽量靠左排列(all levels except possibly the last are completely filled and all nodes are as left as possible)
除末层外各层必然完全填满节点,末层若未满,则所有节点必须保持左对齐 。
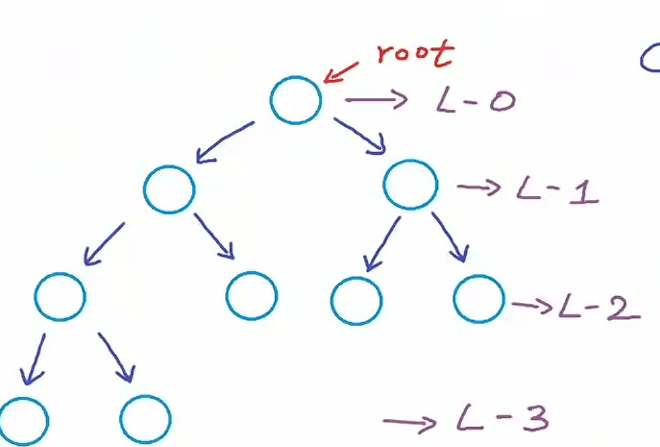
相同深度的节点可归为同一层级
根节点的深度定义为0,节点深度就是从根节点到该节点的路径长度。如图所示,深度为0的节点即第0层节点,记为L0层。根节点下面两个节点位于L1层,再下方4个节点位于L2层,最后这两个节点位于L3层。全树最大节点深度为3,树的最大深度等于树的高度。若将层级编号为L0、L1、L2…,则第I层最多可容纳2的I次方个节点 。L0层最多1个节点(2的0次方=1),L1层最多2个节点,L2层最多4个节点等等,以此类推,所谓每层填满节点,就是每层的节点数必须是最多所容纳的节点个数。因此对于任意层级i,其最大节点数为2的i次方,这是因为每个节点最多可以拥有两个子节点。若每层有X个节点,那么每个节点都可能产生两个子节点,那么下一层最多可以包含2X个子节点。在上述图中,二叉树的第二层有4个节点,这已经是该层的最大值。这些节点每个都可能拥有2个子节点,那么第三层最多的节点个数就是2 * 4 = 8个。
那么对于完全二叉树,除最后一层外所有层都必须填满。最后一层(最深层级)可以例外。该层不必填满,但节点必须尽可能向左靠拢。上述图中的二叉树并非是一个完全二叉树,因为左侧存在两个空缺位置。可以将这个二叉树结构稍作修改,如下图所示,下图中的二叉树结构就构成了完全二叉树。
如果所有层都完全填满节点,这样的二叉树可称为完美二叉树。